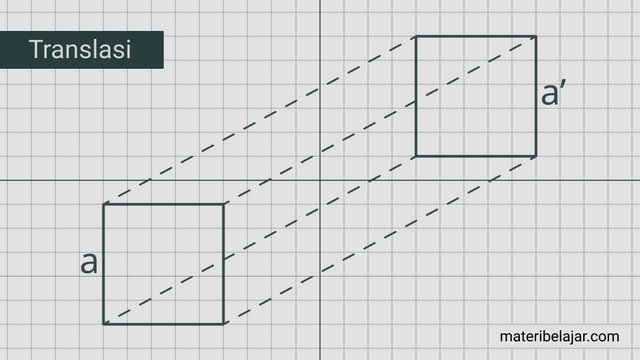
materibelajar.com - Tranformasi Geometri merupakan proses perubahan terhadap suatu bidang geometri dari posisi awal menjadi posisi lainnya yang diakibatkan adanya proses translasi, dilatasi, rotasi dan refleksi.
Pada laman ini kita akan belajar terkait materi transformasi geometri translasi atau pergeseran bidang geometri dengan menggunakan contoh soal pembahasan berikut.
1. Carilah bayangan titik M(7, 6) apabila dilakukan translasi terhadap T(2, 2)!
penyelesaian
M(7, 6)
T(a = 2, b = 2)
menghitung bayangan titik koordinat M:
M'(7 + a, 6 + b)
M'(7 + 2, 6
+ 2)
M'(9, 8)
2. Diketahui titik j(2, 8) dilakukan translasi atau pergeseran sebesar 2 titik ke kanan dan 5 titik ke bawah, hitunglah letak posisi bayangan dari titik koordinat j!
penyelesaian
j(2, 8)
T : 2 titik ke kanan x = 2 dan 5 titik
ke bawah y = -5
T (a = 2, b = -5)
sehingga bayangan titik a kita dapat kita hitung sebagai:
a'(2 + a, 8 +
b)
a'(2 + 2, 8 + (-5))
a'(4, 3)
3. Amati titik b terhadap bayangannya pada bidang koordinat berikut.
Sebuah titik b(-7, -3) dilakukan transformasi geometri translasi menjadi titik b'(8, 2). Hitunglah besar pergeseran T yang terjadi pada titik b tersebut!
penyelesaian
b(-7, -3)
b'(8, 2)
Mencari besar pergeseran T dengan menghitung selisih antara bayangan titik b' terhadap posisi awal titik b.
T = b' - b
= (8 - (-7), 2 - (-3))
= (15, 5)
Diperoleh T (15, 5) yang artinya titik b digeser sejauh 15 satuan terhadap titik x dan 5 satuan terhadap titik y.
4. Sebuah titik P(4, -3, 2) berada pada dimensi tiga dilakukan pergeseran terhadap Q(2, 5, 7) carilah bayangan titik P' setelah dilakukan pergeseran
penyelesaian
P (4, -3, 2)
Q (2, 5, 7)
Sama seperti sebelumnya kita dapat menghitung sesuai dengan rumus, bedanya kita menghitung pada bidang bidang dimensi tiga.
P' = (P + Q)
P'((4 + 2), (-3 + 5), (2 + 7))
P'(6, 2, 9)
5. Sebuah persamaan garis lurus x + y = -3 dilakukan translasi terhadap T(5, -7) hitunglah persamaan garis lurus tersebut setelah dilakukan pergeseran terhadap titik T!
penyelesaian
x + y = -3
T(5, -7)
Mencari bayangan terlebih dahulu dan ubah ke nilai x dan y untuk dilakukan subtitusi
x' = x + 5 → x = x' - 5
y' = y - 7 → y = y' + 7
subtitusikan nilai x dan y kedalam persamaan garis lurus
x + y = -3
(x' - 5) + (y' + 7) = -3
x' + y' - 5 + 7 = -3
x' + y' = -5
Sehingga bayangan dari persamaan garis menjadi x + y = -5.
6. Sebuah persamaan lingkaran diketahui bertitik pusat pada M(-5, 3) memiliki jari-jari sebesar 4 dilakukan pergeseran terhadap titik N(7, 5). Hitunglah persamaan lingkarannya setelah dilakukan translasi!
penyelesaian
M(-5, 3)
N(x = 2, y = 5)
Hitung terlebih dahulu bayangan dari titik pusat persamaan lingkaran tersebut.
M'(-5 + x, 3 + y)
M'(-5 + 7, 3 + 5)
M'(2, 8)
Setelah bayangan dari titik pusat diketahui, kemudian hitung dengan subtitusi kedalam rumus persamaan lingkaran.
M'(a = 2, y = 8) dan jari-jari r = 4
(x - a)2 + (y - b)2 = r2
(x - 2)2
+ (y - 8)2 = 42
(x - 2)2 + (y - 8)2
= 16
Sehingga diketahui persamaan lingkaran setelah dilakukan pergeseran menjadi (x - 2)2 + (y - 8)2 = 16.